Wednesdays, 3pm-6pm, Fall 2024, Fine Arts building room ACW 103 or ACW 102
Instructor: Graham Wakefield grrrwaaa a t york u do t ca
Course material is available at or linked from this website -- bookmark it!
This course is about the astonishing things you can do—and the insights you can find—when you work at the atomic sample-by-sample structure of digital audio. The course focuses on creative exploration of algorithmic and generative sonic signal processing with a special emphasis on “working at the sample level” in real-time/interactive contexts. This means working at the lowest level of time-domain digital audio signals, as is made possible through a software called gen~, that is part of Cycling '74's Max and RNBO. These tools that are widely used for prototyping in artistic and industrial settings including audio software & hardware design, music production, game audio, sonic arts, and other broader contexts.
Audio is one of the primary modalities of digital media art and development. A core emphasis of the Digital Media programs at York is for students to develop their own computational solutions (algorithms and code) to explore creative technology problems most deeply, rather than only relying on available off-the-shelf media and tools. This course specifically serves this aspect – learning how to develop and refine creative algorithms for audio generation and processing, at the lowest level (sample streams) for maximum creative flexibility.
Starting from the simplest beginnings we’ll see how very many seemingly unrelated synthesis and sound processing algorithms come down to a pretty small number of common circuits and useful patterns to think with, that can be reapplied in many different ways to bring new musical signal processes to life.
As the course equips students with techniques and methods in audio synthesis and processing, it could further support students taking courses in sonic arts streams in Music and Digital Media. As it develops awareness and understanding of the potential of digital signal processing it could lead students to continue to take up more advanced signal processing courses in EECS.
For clarification: this is not a course about music composition, performance, or studio production as such; nor is it a course in mathematics and engineering for digital signal processing. No background in music theory, mathematics or computer science beyond high school levels are assumed. The curriculum is primarily practice-based: problem-driven and technique-focused leading toward applications that you can utilize in other project-based courses, research, compositions, and artworks.
Prerequisite: DATT 2050 or by permission of the instructor.
Note: 2024 is the first year the course runs, so it will be somewhat experimental as we learn what works. As such, the weekly content will be fleshed out adaptively over the next few weeks.
Course textbook
The course follows the structure and assigns readings from the textbook “Generating Sound & Organizing Time”, Wakefield G. and Taylor, G. Cycling ’74, October 2021. ISBN-10: 1732590311 / ISBN-13: 978-1732590311
Course software
We will work using the gen~ environment within Cycling '74's Max. All students have access to a license for Max supported by the course fees.
License codes should be coming to all students by Sep 11th.
The computers in ACW 102 also have Max installed and licensed, and students can come in to use them during open lab hours.
Evaluation
Sep 4
Hello and welcome!
https://docs.google.com/presentation/d/1xrXM86cCE7vzykYYdINs1G9g9f7FaeiiZd6IRlKBEjI/
Get things installed
Make sure you have Max running, and can edit a gen~ patcher.
Be sure to also install the additional patches that come with the book (the download link & instructions are on page 3.)
Let's patch
Get to know some of the most commonly used gen~ operators. How to find out about operators while patching.
Make sound: noise, cycle, *, +, etc.
Get some parameters to control it
Get to know how to visualize the signals in a patch, to help understand what's going on.
It's always handy to have some extra out operators for debugging purposes! It can also be handy to have some example input sounds to work from. Here's a template patcher with some of these already set up:
Homework
scale, clip and wrap are especially useful. switch and gate/selector and latch and mix history (single sample) or delay (many samples)accum, counter and phasor. See also delta and change. buffer and data, peek/sample and pokecodeboxgen (and saving as external gendsp files)Resources
Background
Community
Sep 11
Let's work through the first patches of Chapter 2
+ and history. Toggle to enable. / samplerate for seconds.switch to rewind, click~ to trigger it. accum operator. buffer~ and referencing it in gen~, reading with peekwrap operator, param duration or buffer lengthsample and a 0 to 1 scale, so use wrap 0 1/ samplerate. Now we have built the phasor operator.Discuss the merits of phasor ramps over triggers for rhythm & cyclic time
Make a patch that can generate new ring tones for your phone. This is a generative patch: each time the patch runs, it produces a ring tone that sounds a little different. Your ring tone will be 25 seconds long. It can be stereo if you want, but mono (single channel) is fine -- not all phones have stereo speakers.
Be sure to follow all the general procedures for assignment patches
Start from the template patch here: press the button below to copy the patch to your clipboard, and then open Max and select File -> New From Clipboard, then save that patch as "assignment1.maxpat":
If you want to put this ring tone on your phone:
gen~ @title myname, not gen~ myname. Similarly, if you want to name a subpatcher inside the genpatcher, use gen~ @title myname, not gen myname. This will ensure that all your work is in one patch. buffer~ test jongly. The built-in sounds include: ahkey, anton, bass, brushes, cello-f2, cherokee, cym, drumloop, duduk, epno, eroica, huge, isthatyou, jongly, rainstick, sacre, sfizz_help_loop, sfizz_help_vibes, sho0630, talk, and vibes-a1. Your project shouldn't depend on any other sound files to work. 1. turn audio on, 2. press this button, 3. wiggle this parameter. Assignment 1 due Sep 21
Sep 18
wrap 0 1: see ramp_ratchets.maxpatfloor (go.ramp2steps): see ramp_steps.maxpatwrap 0 1 (go.ramp.rotate): see ramp_rotate.maxpatgo.ramp2slope) and getting information from the ramp's slope (go.ramp2freq): direction, phase within cycle, Hz, BPM, period, time until next cycle, etc: see ramp_slope.maxpat. go.ramp2trig), which you can use to start a sound, sample an input, etc: ramp_to_trig.maxpat. go.ramp.div.simple, or go.ramp.div and go.ramp.mul: see ramp_div.maxpat then ramp_divisions.maxpatPatching together deep dive: Chapter 3 Unit Shaping / From ramps to LFOs
triangle or go.unit.triangle shapers, with duty-cycles, including morphing from ramp to triangle to reverse ramp! latch and go.ramp2triggo.unit.sine)> operator) to derive a pulse, along with pulse duty parametergo.unit.trapezoid)go.lfo.multi)Sample & hold for random steps, LFOs and glides
The latch operator with go.ramp2trig means we can create arbitrary stepped sequences.
noise for a classic rhythmic sample&hold signal. See Chapter 3 first few pages; Ch4 random_steps.maxpatscale the noise to get a desired range (Ch4 random_range.maxpat)noise using a * N, floor, / N sequence (Ch4 random_integer.maxpat)What if we don't want it to jump between steps, but instead to glide between them?
latch. (See Chapter 2 "Shaping smooth-stepped interpolation")go.unit.sine. change for. accum ramp into a clip 0 1 to stop at 1. Retrigger the accum ramp when the target changes (via change). This is a basic line generator (see Ch6 slide_slew_and_line.maxpat). We can smoothly shape the ramp too, see Ch2 interpolating_glides.maxpat. Sep 25
Reviewing Assignment 1 & the sounds
What is noise?
go.svf.hzRandom techniques (ch4) -- we covered most of these last week, but maybe build a random walker to review?
noise -> scale. Or, for a 0..1 range, noise -> abs. noise -> scale -> floor, and go.random. noise -> abs -> < chance (maybe -> latch), where "chance" is from 0 (no chance) to 1 (sure thing). Use go.chance. random_chance.maxpatnoise -> latchlatch seqeuence into mix as we saw last week. Can chain this into a longer interpolated curve: random_smoothed.maxpatwrap, clip or fold the count to keep it in a usable range. What is chaos? An algorithm producing a deterministic yet unpredictable trajectory. Tend to have recognizable patterns of behaviour but never quite exactly the same. This can make them perceptually interesting, especially for modulations. Another way to ride the line between tedious repetition and incoherent randomness.
Lots of different chaotic algorithms are known, and many included in the book (see the go.chaos subfolders)
Focus example: Lorenz attractor
Most of them are essentially accumulators that are cross-coupled, so they have multiple simultaneous outputs.
Output ranges can be very different for different algorithms; but we can use an "auto-limter" patch to keep things in our desired range
Example: loosening up a clock: chaos.tempo.nonrobotic.maxpat
Example: injecting audio into a chaotic system chaos_Lorenz_audioinjection.maxpat
Continue to Chapter 5: Stepping in Time
A lot of sound synthesis technology innovation has been inspired by science fiction, or indeed has pioneered science fiction! Sometimes these are also built from very meager resources. A wonderful example is the soundtrack of the film Forbidden Planet from 1956.
"Forbidden Planet's innovative electronic music score (credited as "electronic tonalities") was composed by Bebe and Louis Barron. It is credited with being the first completely electronic film score, preceding the development of analog synthesizers by Robert Moog and Don Buchla in the early 1960s. Using ideas and procedures from the book Cybernetics: Or Control and Communication in the Animal and the Machine (1948) by the mathematician and electrical engineer Norbert Wiener, Louis Barron constructed his own electronic circuits that he used to generate the score's "bleeps, blurps, whirs, whines, throbs, hums, and screeches". By following the equations presented in the book, Louis was able to build electronic circuits that he manipulated to generate sounds. Most of the production was not scripted or notated in any way. The circuit generated sound was not treated as notes, but instead as "actors".
The assignment: Create your own "electronic tonalities" for an alien world, e.g.
Be sure to follow all the general procedures for assignment patches -- especially remembering to make sure that everything that generates sound and structure is contained in your gen~ patcher, and your patch does not have any external dependencies!
You are free to re-use any patches from the textbook, or from the Help/examples/gen folder in Max. Here's the starter-patch:
Assignment due Oct 9
Please submit Assignment 2 here
Oct 2
We can create melodies by mixing scaled gate signals e.g. mixer-sequencer.maxpat. Or take some chaos, feed it through a comparator, and mix those.
We saw the basic sample & hold sequencer in week 2 (latched-sequencer.maxpat), and the basic shift register (shift-register.maxpat)
A quick primer on pitch, and how we represent pitch in signals
phasor and cycle work with frequencies in Hz, meaning repetitions per second. But we are used to thinking about pitches in octaves, semitones, etc. What's the relationship?pow(2, N) or simply exp2(N). pow(2, 13/12), or exp2(13/12). That's a lot harder to remember! So some synthesizers use a different scale called "volt per octave", where adding 1 volt of level means going up one octave, which is multiplying the frequency by 2. Quantizing
floor or round)round operators for inversion & transposition.See quantizing-pitch.maxpat
Deep dive: We can combine those ideas into a more complex generative sequencer, based on the Klee Sequencer:
go.shiftregister8, which is clocked by a phasor -> go.ramp2trig, for example. xor of the last step with some chance control: shift-register-weighted-xor.maxpatDepending on time, we could deep dive into another looping sequencer -- the urn model from Ch4
Deep dive: Euclidean rhythms: an algorithm to distribute K events over N steps as evenly as possible. It happens to produce a lot of rhythmic motifs common in musics from around the world. Also prevalent in techno.
floor, multiply by K/N for the desired slope, quantize again with floor for the Euclidean steps. Send these through change -> bool for triggers.ceil of quantized * N/K) and our next step (same but for quantized+1) are, the difference of which is the number of beats in the event. phasor * N ramp, subtract the current step, and divide by the step length, to get a 0 to 1 ramp. [We could have used a scale operator there.]latch operators. Lots of other possible refinements, e.g. what to do when K > N. Timbral shaping via sigmoids (end of Ch3) to turn a simpler signal into a more complex one.
tanhtanh, see the go.sigmoid.* abstractions in bipolar_waveshaping_sigmoids.maxpatgo.unit.sigmoid.*Timbral shaping via quantizing (bitcrushing) -- last section of Chapter 5
(Basically, it can be worth experimenting whether a process we use for control signals might also do something interesting for audio signals!)
Today's patch:
Oct 9
In almost every class since the first week we have encountered a simple lowpass filter. Most often we have seen the filter as a mix and history pair, which is known as a one pole filter, but if we dig into the algebra of this a bit, or rather, if we re-arrange the patching a bit, there's a few other ways of seeing what this is.
(See onepole-explorations.maxpat for examples of most of the ideas below.)
mix operator is just a weighted average between two inputs a and b. If the mix is in the centre, when the mix amount t equals 0.5, then this is a*0.5 + b*0.5, which is the same as (a/2+b/2), which is the same as (a+b)/2, which is what an average of two numbers is. A weighted average skews the balance more to input a or input b, but makes sure that the sum of the weights is still 1.0. That means a*(1-t) + b*t, which is exactly what mix does. mix operator to a * t and * 1-t and +, we should be able to see the feedback loop through a + operator makes an integrator or counter, just like we saw back in the first week. But this integrator is leaky, because while we are counting up we are also scaling the count down again with * t. b? Now we are averaging the input with the past history of a signal. The higher we set t, the more weight we give to the history. Averaging a signal over time is going to smoothen it out, which means fast oscillations will be softened more than slow oscillations. That's why higher frequencies are reduced more than lower frequencies, so it is a low pass filter. a*(1-t) + b*t into t*(b-a) + a. If you look at this as a patch and follow the path from the history b onward, first we subtract a (getting the value of b relative to a, which is a translation, or difference), then we scale that difference down a bit, then we translate it back from being relative by adding a back on again. So this is a kind of translation. We project b into the point-of-view of a, reduce it, then project it back out of the point-of-view of a. Intuitively, what this is doing is trying to make b get closer to a, which means our history is constantly trying to get closer to our input, as if chasing it, but it can only catch up sluggishly. And that's another way to understand how it will smoothen the signal out. What's the difference between a signal and its lowpass-filtered copy? If the lowpass smoothens it out, then what's removed is all the fast, noisy movements. This difference, or residual, is the original signal with all the low frequencies removed, leaving only the high frequencies behind -- which is a high pass filter. It's as simple as input - lowpass. It does the opposite of averaging, and the opposite of integrating, which is differentiating. It doesn't follow the trend of the input, it gets distracted by all the input's skittish movements.
dcblock operator just for this job.Setting the frequency.
The parameter t has to be very close to 1.0 to have a significant effect on a gate signal. The closer it is to 1.0, the smoother the output, the deeper the frequency filtering. Often we measure a filter's response in terms of a "cutoff frequency", which is the frequency at which the input will lose half of its power. The math to compute the parameter t in terms of a cutoff frequency is: exp(-twopi * hz/samplerate).
Filtering a gate into an envelope
We can apply a onepole filter at sub-audio frequencies to shape control signals, such as smoothening a gate signal into an envelope. At these low speeds it isn't as intuitive to set a frequency in Hz. Instead, if we want to set a decay in seconds, we can use t60(seconds * samplerate). This will set the time at which an input impulse will decay by 60db, which is about 0.001. That might be useful if we want to use our filter to filter very slow events, like a note on/off gate. Filtering a gate like this can produce natural envelope shapes for a sound.
Once you have a nice envelope you can multiply this by a sound to make it's level naturally appear and fade away.
In this case it often makes sense to have it rise quickly but fall slowly, because that's a natural shape for many sounds. In that case, we can switch between different filter coefficients depending on whether the input is greater than the filter's output (via the history) or not. The slide operator in gen~ is basically doing this. Or, we could directly use the input value to mix between different coefficients (being careful to clip 0 1 of course).
Low pass gates
Slews and lags/lines
Aside from using onepole filters, there's some other kinds of smoothening and filtering that are especially useful at sub-audio rates. One drawback of the onepole filter (and most recursive feedback filters) is that they never quite reach their target -- the response curve is logarithmic so it's always just slightly closer but not quite there. What alternatives are there for smoothly approaching a target but also definitely arriving there? See slide_slew_and_line.maxpat
We saw one already several times: we can mix from a latched output to a latched input. In this case we can drive the mix by an accum @resetmode pre into clip 0 1. And we can retrigger the latches and accum whenever the input changes. The input to the accum sets how long it takes to reach the target. This is a line generator or lag generator, and it is what go.line.ms and go.line.samples do.
A different option is to have the filter always approach the target but give it a speed limit; that's called a slew limiter. In that case, we get the difference between the input and our current state (history), which tells us how much we need to move, but then we clip that amount to a certain negative & positive maximum speed, and add that clipped speed to our state as the output. This ensures we will reach the target, with a maximum speed, but how long it takes to get there depends on how far away the target is.
Allpass filters
Crossover filter
What if we want to take a sound and split it into two signals, one with the lower frequencies and the other with the higher frequencies, so that we can process them a little differently and then mix them back together? For example, we could use this to create a kind of bass & treble tone control, or to apply distortion only to higher frequencies, or to pan them differently, etc. This is where we need crossover filters.
A proper crossover is one where adding the outputs together reconstructs the same energy spectrum as the original input sound. (Which is an allpass response).
As we saw in the onepole-explorations.maxpat patch, we saw that the filters apply phase changes to the input signal -- it changes the spectrum and also the wave shape. That change in phase response is what made it create "phaser" effects when mixed back together, and that's exactly what we want to eliminate in a crossover.
It turns out we can use an allpass filter at the same frequency to exactly match the phase response of two cascaded one pole lowpass filters. By subtracting their difference we get a high pass filter that exactly matches the lowpass, and we can add them together to recover the original spectrum. See crossover_simple.maxpat.
If we want to get more than two bands, we can do the same process again -- the only thing we have to remember to do is that whenever we lowpass filter one stream, we have to apply a matching allpass filter to all the other streams. See crossover.maxpat for a 3-stage crossover.
Biquad filters
go.biquad.coeffs. See biquad-coefficients.maxpat and biquad-coefficients-shelf.maxpatTrapezoidal filters
However a drawback with some of these filters, such as the biquads, is that they don't modulate very well, and can sound nasty and blow up easily if their coefficients are changed suddenly or rapidly.
This partly comes down to the integrators at the core of their design, which are Euler-style integrators: they add and then output the count. This means that they combine signals that are biased to the past with signals that are biased to the present.
Instead we can turn to a different different kind of integrator, called a trapezoidal integrator. Whereas Euler integrators are biased either to the past or the present, a trapezoidal integrator balances both as a kind of average. It's a kind of linear approximation of the value half-way through a sample. See integrators_and_filters.maxpat
So how do we build a filter out of this kind of trapzoidal integrator? The math and patching needed to create a one pole filter from this is a slightly more complex than from the Euler integrator, but not really any more expensive, and it handles audio-rate modulation much better. See trapezoidal-onepole.maxpat
State variable trapezoidal filter
A wonderful example of the trapezoidal method is the state variable filter (e.g. go.svf), which, similar to biquads, can produce many different output spectra, but it does them all at once, and can be modulated at audio-rates very nicely. This will be our go-to filter most of the time. See trapezoidal-state-variable-filter.maxpat
Oct 23
What is a digital delay?
In a way it is a bit like a long chain of history objects, each one delaying the input by one sample. But it would take tens of thousands of these objects to get an echo of one second; and we don't want to have tens of thousands of objects running in a patch! Instead we can use the delay object, which does things much more efficiently. For example, any signal sent into a delay 10000 object will come out of the output 10000 samples later.
It is helpful to think of a delay as a loop of memory.
So, instead of moving the data around, we move the reader & writer around.
In computer science, this is often called a "ring buffer" or "circular buffer", and it is used in many different applications, such as thread message passing and input event handling:
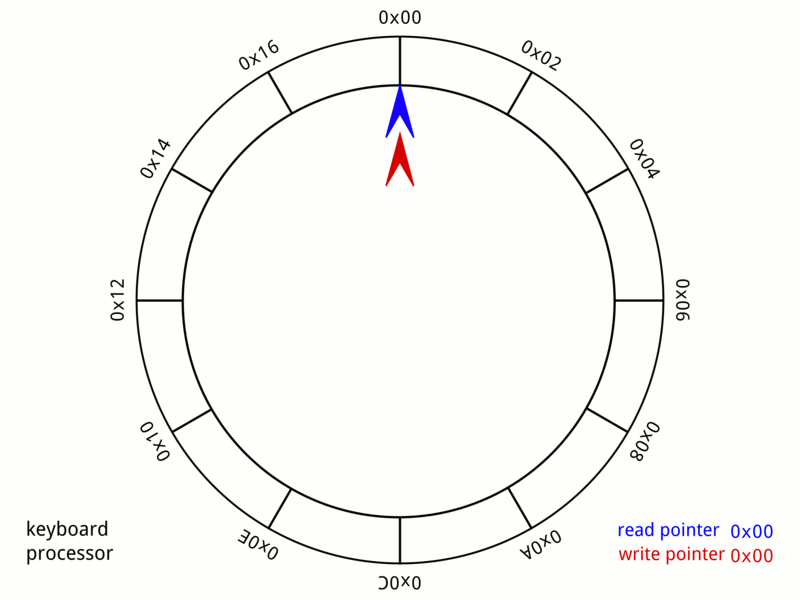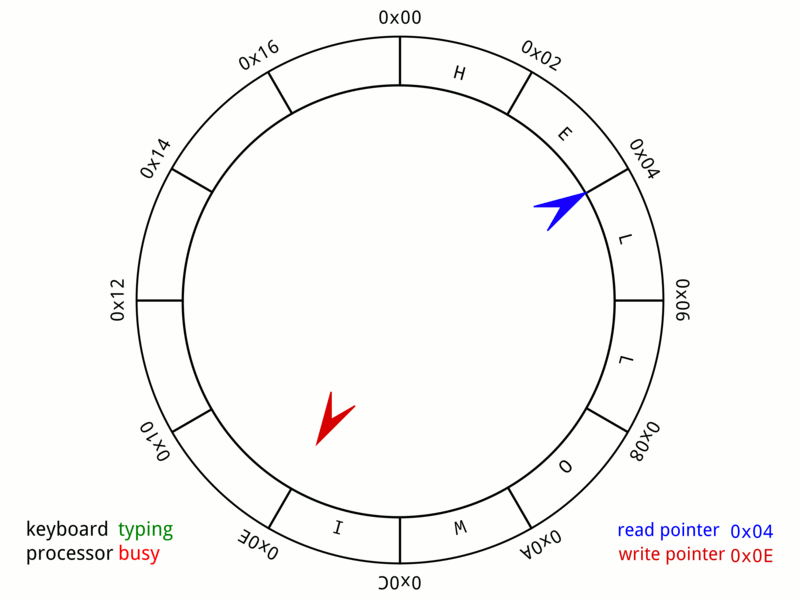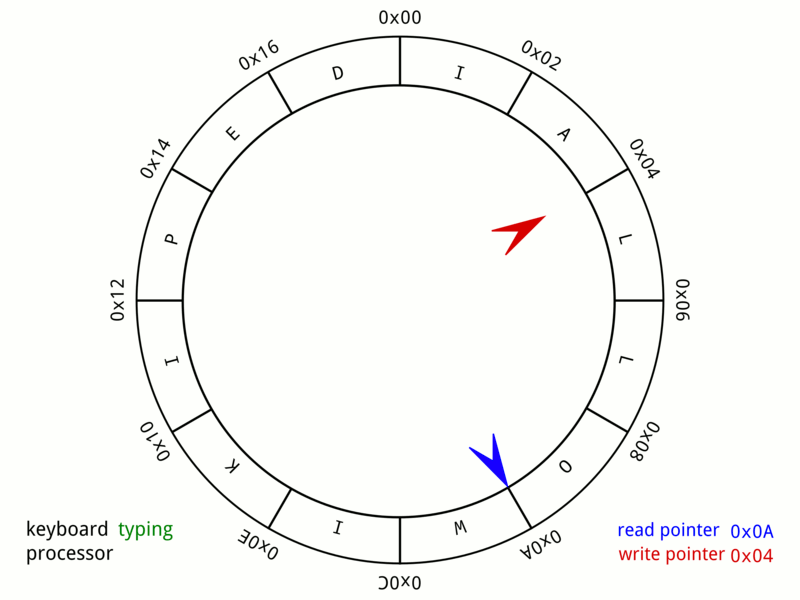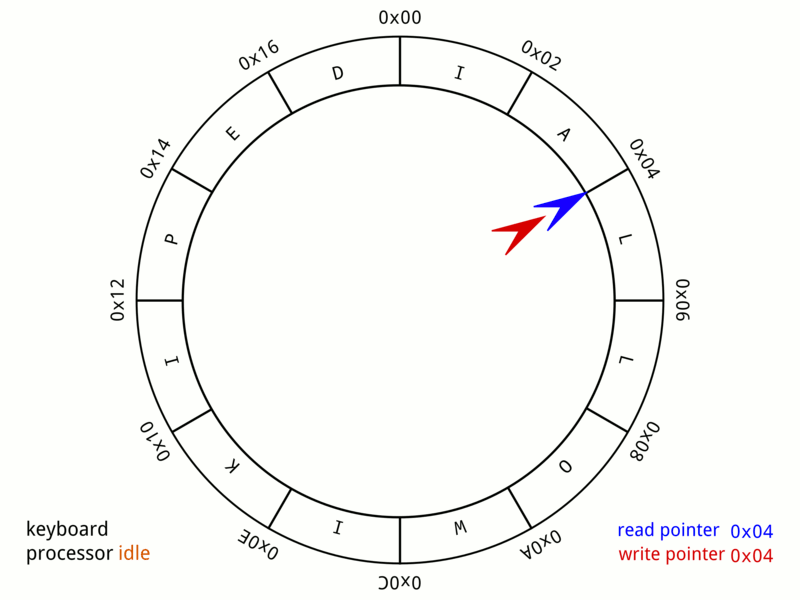
The main difference is that in a digital audio delay, the write point always moves at the current sample rate, one step at a time. (Another difference is that in audio delays, we can also have multiple readers, called a "multi tap delay")
What kinds of sounds can you get from a delay? Take a look at the delay_multi_effect.maxpat patch and spend some time playing around, there's a huge range of possibilities!
Then let's build our way up to that.
The gen~ delay operator takes an argument to say how many slots the loop has. This length effectively sets the maximum delay time, in samples. If you want to set it in seconds, e.g. for up to a 4-second delay, you could write delay samplerate*4. If you don't specify it, it defaults to one second.
You can also change the delay time dynamically through the 2nd inlet (this is also measured in samples); this can be anything less than the maximum delay you specified when you created it.
The delay operator also has a 2nd optional argument for if you specify more than one reader tap. E.g. a delay 1024 4 will have four read points, and you'll get extra inlets to set their delay times, and extra outlets for their audio.
* samplerate. To set in milliseconds, you can use ms -> mstosamps. mix it with the input signal. See delay_feedforward_basic.maxpatdelay operator allows feedback loops just like history does. E.g. set the input of the delay to be the output of the mix between input and delay. See delay_feedback_basic.maxpatDid you notice that this looks a lot like the
mix+historyone pole filter we have seen so many times already? It's exactly like a one pole filter, but just stretched out over time. You can also turn other classic filter structures into delay structures by replacinghistorywithdelay.
If you get an echo going then set the feedback balance to 1.0, it becomes an endless looper. But now the input is unheard.
Instead we can use the mix as a wet/dry balance control, and use a simple multiplier for our feedback control, adding both input and feedback to the delay.
To set a decay time, we can use the t60 operator just like we did for the low pass gate. Remember, t60 is for feedback multipliers. But we should divide the decay time by the delay time before sending it to the t60, because we will do one multiply per loop, not one per sample. See delay_feedback_decaytime.maxpat
A lot of the character of a delay depends on what other kinds of processing we put in this feedback loop.
What about modulating the delay? You might notice that it can often lead to clicks. As usual, we can smooth the stepped quality of parameter changes using a simple onepole, or slide, or a slew limiter, or lag generator, etc. These basically smoothen out any sudden changes of levels in a way that is mostly imperceptible.
However there's one parameter for which this is not the case. If you smoothen out changes to the delay time, you'll start to hear pitch changing effects. See delay_morphed_times.maxpat. These are like the Doppler shifts when a sound is moving toward you or away from you (in this case, it is the reader & writer that are moving towards each other or away.) This is relativity! The pitch shift is exactly proportional to the slope (the "velocity") of the signal that controls the delay time.
That patch also shows how you can calculate what the pitch change will be, or vice versa, how to control the pitch change in a desired way!
What if you want to change the delay time without any pitch artefacts at all? The only way to get around relativity is to create a second delay (or a second tap of your delay), and crossfade between them. It's a sleight of hand: whichever one is currently silent in the crossfader, we can change the delay time however we want, and then quickly crossfade over to it -- quick enough to not be distracting, but not so quick to click. The patching to do this is a little trickier, but the core of it is a very handy little circuit that we will use again as go.background.change. See delay_morphed_times_no_pitch_change.maxpat
Delays of around 0.05ms to 5ms (equivalent to frequencies of 500Hz to 20kHz) have almost filter-like effects. These are often call "comb filters" because the spectrum response has teeth like a comb. See comb_filter.maxpat
With delays of 0.5 to 25ms, we are in the region of pitches, and with enough feedback these can sound a bit like a stringed instrument. This is usually called Karplus-Strong synthesis. See string_basic.maxpat
kslider pitch), use mtof to get the frequency in Hz, and then !/ 1 to calculate the period in seconds (as 1/frequency), then multiply by * samplerate to get a period in samples. (Or combine the last two operations as !/ samplerate). See string_pitched.maxpatt60 method as before. See string_feedback_control.maxpat2*log(1 - b), where b is the filter coefficient. See string_damping.maxpat. delay. Remember the delay loop is a ring of discrete memory slots. If we ask for a delay time of 2.5 samples, do we read from sample slot 2 or slot 3? delay will return the weighted average of the two nearest memory slots, which is linear interpolation, the same as we used with the sample operator before. But as we know, averaging is also like a low pass filter. The mixing of two nearest slots is what is causing the apparent damping. delay @interp none sounds much worse. There's no simple and cheap solution here, but there are a few different kinds of interpolators that you can try with different tradeoffs. See delay_interpoation_types.maxpat for some examples. Generative Radio Station!
Have you ever heard Generative.FM? It is a collection of generative radio stations that never end or repeat. It could be music for working to, sleeping to, meditating to, focusing to, ... and never getting bored from. (It's not the first generative radio station ever, there have been quite a few, but it's the most active one I could find today)
This assignment is to create a robot radio station, which is always absolutely different every time you listen in.
To ensure it is always unique, the patch should use the current date and time to modify its parameters. The template patch below has this already set up for you. You can either listen to the current date & time, or pick a random date & time (or choose by hand), to make sure that the station has enough variety.
Most of the stations at generative.fm are pretty ambient, and might be a bit too slow and sleepy. Let's make stations that are a little more upbeat. The template patch has a clock source built in (with bar and beat phasor ramps). Use this to drive for some element of your station -- maybe a backbeat, maybe a melody, maybe an LFO pattern, etc.
Before building the patch, spend some time researching among the example patches drawn from the textbook or from the Max / Help -> Examples -> gen folders. Spend some time playing with many of these patches until you find three or four that you think you can work with. Your radio station must combine these patches together in a way that you (and your friends) can listen to for a long time. You can modify these patches as much as you want, and you are recommended to add more processing of your own to make it uniquely yours.
Later, we will use RNBO to embed these patches as running code in a class website. In order to do so, we have some specific rules for the assignment:
gen~ @title CLOCK_RADIO patch. gen~ @title CLOCK_RADIO patch, and connect them up. dcblock -> tanh -> out section at the bottom of gen~ @title CLOCK_RADIO patch. If your output is mono (not stereo), route it to both of them. Aesthetic requirements:
And all the usual general requirements for assignments
Comments:
Here's a quick example radio station, based on a couple of patches we have already looked at
Assignment 3 is due on Nov 10. - Submit the Max patch via this form here
Here's the assignment 3 template patch:
Oct 30
Thinking ahead about final project
This chapter is all about modulating one oscillator by another.
Many times we have seen multiplying a signal by some other constant to set its apparent loudness, or multiplying by an envelope to shape the loudness over time. Try multiplying an audible sine wave (e.g. cycle 200) by a low frequency oscillator (LFO, e.g. cycle 2). You might want to scale -1 1 0 1 to get the LFO to be unipolar, just like an envelope. Now try raising the frequency of the LFO into audible rates, and listen to what happens.
Look at it on the spectroscope~ -- what can you see?
These new frequencies are called sidebands. If you scaled the second oscillator to be unipolar, this is Amplitude Modulation (AM). If you didn't, and you directly multiplied the two signals, it is Ring Modulation (RM). Actually you can pretty easily mix betwween these two, see AMRM.maxpat.
With AM and RM, the new sidebands are the sum and difference of the two input frequencies. If the input signals are more complex than sinewaves, then there will be sums and differences for every frequency component in each signal -- that can get complex fast. But we're going to look at things that get even wilder.
To do that, first let's break apart the cycle operator into its subcomponents: phasor -> * twopi -> sin. Now we can modulate the oscillator in two different ways: we could modulate the frequency of the phasor to get Frequency Modulation (FM), or we could modulate the phase going into the sin, which is called Phase Modulation (PM). The amount of modulation we apply is scaled by a multiplier called the modulation index -- often driven by an envelope. See FMPM.maxpat. With simple sines in this way they sound the same, but as we make things more complex they diverge.
Look at the spectroscope~ now, and you'll see a cascade of new sidebands. The higher the modulation index, the more of these sidebands appear. The main oscillator (the carrier) is still present, but there are additional frequences above and below, spaced by the frequency of the modulator oscillator.
So, if you want a harmonic sound, you'll want the carrier and modulator frequencies to form a simple integer ratio (or near-integer ratio). One way, encouraged by FM pioneer John Chowning, is to establish a base frequency, and then make both carrier and modulator be (integer or near-integer) multiples of that base frequency. See FMPM-harmonicity.maxpat). When this happens, the many sidebands tend to line up with each other in a way that creates a much less "clangorous" sound.
Digital FM synthesizers became popular in the 1980's (actually they were PM synthesizers but marketed as "FM" for historic reasons). Those synthesizers often used more than two oscillators -- four or six were typical -- and you could arrange these in different structures, such as multiple carriers sharing modulators, or multiple modulators controlling a carrier, or cascades of modulators modulating modulators modulating modulators modulating carriers etc. Each of these "algorithms" has different sonic potentials. See the example patches.
Looking at FMPM-cascade-modulation.maxpat when the modulator is modulated it becomes more complex than a simple sine wave, and now we can start to hear and see the differences between PM and FM. Or, for a more complex waveform, try looking at just how different a triangle-wave modulator affects FM and PM. Slow down the triangle wave to sub-audio rates so we can look at the signals. What you see is that while in FM the level of the modulator directly affects the apparent output pitch in FM, with PM it is the rate of change of the modulator that affects the apparent pitch. That makes sense, because we have bypassed the integrator in the phasor.
That is, to turn FM into PM, you just need to integrate the modulator. The FMPM-blending.maxpat shows how we can make them exactly equal by passing the modulator through a low pass filter (a leaky integrator) for PM, and through a matching high pass filter (a leaky differentiator) for FM. Actually filtering like this is a good idea in general for other reasons:
Some synthesizers also offered feedback algorithms: taking the oscillator's output and using it to phase modulate itself, via an "index" multiplier. Here the spectrum is less symmetric, and it can produce sawtooth-like waveforms. But the feedback multiplier is very sensitive, and it can quickly become chaotic noise. We can tame that noise a little by placing a filter in the feedback loop -- see FMPM-feedback.maxpat. This is a pretty rich oscillator for how simple it is!
It gets even richer when you place feedback oscillators into bigger structures. One of my favourite patches in the book is simply two of these oscillators feeding back into each other -- see PM-cross-feedback-filtered.maxpat
But don't stop there -- these AM, RM, FM, and PM components are like LEGO, you can just keep combining parts into bigger structures. Try inserting other weird stuff in there too -- wavefolders, bitcrushers, delays, etc. See for example FMPM-waveshaping-modulator.maxpat, or for a more unusual example, PM-asymmetric.maxpat
Actually there's another way of looking at what phase modulation is -- as another kind of waveshaping! No matter what phase signal we send in, the output will always be somewhere between -1 and +1. This is especially true when the carrier frequency is 0Hz -- then we only hear the modulator's frequency, and the index is like a brightness control.
With all of AM, RM, FM, PM, the addition of sidebands might create very low (inaudible) frequencies, which you might want to filter out with a DC-blocking highpass filter.
It can also create incredibly high frequencies, which are much too high to be represented at our samplerate. Unfortunately in a digital system, there really is a limit to how high of a frequency you can represent -- this is the Nyquist limit which is samplerate/2. Any frequency generated above this will alias, which means, it folds back down below samplerate/2 again. Here's a visual way to understand why aliasing happens:
These aliasing frequencies are usually inharmonic, and often undesirable -- part of the reason why analog synthesizers are sometimes preferred over digital ones. Unfortunately you can't just use a filter to remove these frequencies after they have been generated, because they have already aliased at that point. Instead we have to modify our algorithm so that aliasing frequencies are not generated in the first place.
Instead we either have to increase the samplerate (such as by oversampling -- which is complex and not covered in this course), or modify the input modulator/carrier waveforms (e.g. by filtering) to limit how high their frequency content is, and thereby limit the sidebands. See AMRM-bandlimited.maxpat. For FM/PM this is complicated by the modulation index, but see FMPM-carsonrule.maxpat or FMPM-carsonrule-filtered.maxpat for solution that work with sine waves, and FMPM-antialias-filter.maxpat for a more general solution.
We saw last week how delays can create pitch shifts through Doppler effects, and if we modulate the delay time quickly this can create warbling effects. This is in fact also a kind of phase modulation! The PM-is-doppler-delay.maxpat patch demonstrates what we need to do to convert a simple PM patch into one that works with delay -- including keeping the modulation signal above 0 (because delays can't read the future), and converting the phase in radians to a delay in samples. One of the benefits of using a delay is that now we can phase modulate any singal at all; but one of the disadvantages is that, to make it equivalent to regular PM, we need to know the frequency of the carrier.
You may have noticed that FM and PM often produces complex inharmonic "clangorous" tones. But there's a way to get all the fluidity of FM/PM and yet stay completely harmonic, if you want. The trick is similar to how we solved changing delay times without pitch shifts: we replace our single gliding sine oscillator with two integer harmonic oscillators and crossfade between them instead. See Harmonic.maxpat. The go.harmonic abstraction can be dropped in as a replacement for the sine oscillators at the heart of all the patches we have seen before -- compare AMRM.maxpat with AMRM-blended-harmonics.maxpat for example. See also PM-blended-harmonics.maxpat, and ModFM.maxpat.
Nov 6
Final project discussions
Radio discussions
SynthUX Hackathon -- do you want to help organize one at York University?
Longer-term projects -- do you want to do things in the Alice Lab?
Continuing from last week, from PM feedback onward.
Some requirements:
You should have your proposed idea ready for next week!
Some more detail on ideas:
Perhaps a few of you want to design instruments and make a "gen~ band" (or "gen~ ensemble") to perform together?
File -> Show Package Manager, search for "Link", install) and once installed, you can create a link.phasor~ object that will give you bar and beat phasor ramps you can route into gen~; and anyone on the same local network will be synced to the same tempo. Link also works with Ableton Live of course, and also VCVRack, SuperCollider, tons of Android and iOS apps, TouchDesigner, TidalCycles, and lots of other interesting software, and also some hardware devices too -- see list here. Web-based data sonification:
Sounds for a project in another course
Or something else -- tell me your ideas!
Nov 13
Back in chapter 2 we saw how to play a buffer~ with the sample operator, using linear interpolation to estimate the values between samples. Remember, linear interpolation is just like a mix crossfade.
When the phasor playing a buffer is an audible frequency, this dominates the apparent pitch, while the buffer content determines the waveform and timbre of the sound. This seems incredibly flexible, but the buffer data is static.
To work around this, many synthesizers packed multiple waveforms into a single buffer, so you can select different subsections at any time. This is a wavetable.
In gen~ we can use the wave operator to jump around different parts of a wavetable. See wavetable_1D.maxpat and the building subpatchers. We just have to be careful to pick the right subsets. For example, if a buffer contains 64 waveforms (like wavetable64.wav does), then the length of each waveform is dim(tables) / 64. The wave start index must be an integer multiple of this length, and the wave end point should be the next integer multiple. It's important to understand this -- we'll end up expanding this idea into 2D and 3D sets of waveforms later!
To smoothly morph between two adjacent waveforms, we can use two wave players and mix between them. E.g. If the wave selection value is 3.4, then we mix 60% of wave 3, and 40% of wave 4.
These ideas extend to 2D:
wrap 0 N). The sample index is then "len" * X * (Y*8). wave operators and bilinear interpolation -- which means two mix operators for each X pair into another mix for the Y. Of course we could take that to a 3D volume too:
wave operators; and three layers of mix operators to morph them. A related approach to 2D wavetables is to create wave terrains. In this case, there is a 2D space in which each cell is a single sample, rather than a single waveform. You play a wave terrain by traversing a path through it -- which is sometimes called an orbit. We can re-use a lot of the patching from the 2D wavetable -- for computing indices and doing bilinar interpolation. For a simple orbit, we can use the poltocar operator, which generates X and Y pairs from a radius and angle. See waveterrain_2D.maxpat.
To generate terrains we'll need to dig into a codebox for nested for loops -- one loop for X and another for Y. See waveterrain_generate_codebox.maxpat. Or, we can make use of Jitter matrices to generate terrains, see waveterrain_generate_BFG.maxpat.
A lot of the interest in wave terrains is in the orbit design. You may notice that a wider radius tends to create a brighter sound, as it takes in more data points over time. We can build more complex orbits using multiple poltocar operators, and apply different operations to deal with X and Y values that may go out of range, such as fold, wrap, clip or tanh (or other sigmoids). See wavetable_2D_carom.maxpat.
The math here is really open-ended. One interesting example is an algorithm to generate a variety of polygonal orbits. See polygonal.maxpat.
Note that all of these oscillators could be inserted into any of the FM/PM algorithms we enountered before.
Let's look at the wavetable oscillators again. So far our wavetable operators are using linear interpolation to smoothly estimate the values between samples. That's a lot better than no interpolation at all, but it is far from perfect. If you start using rich harmonic waveforms like sawtooth shapes, and place them under extreme modulations, you will probably start to hear digital aliasing.
To reduce this aliasing, we can use sinc interpolation (blue) rather than linear interpolation (red).
But aliasing can still happen for playback of discretized sample data at different rates:
To handle the case when the buffer contains too much data to represent, we can use mipmapping:
This means reapeatedly decimating the data in powers of two -- but we can achieve the same result just by quantizing our buffer lookup accordingly:
This is quite a deep topic and you should refer to the textbook for full details. See wavetable_sincmipmap_sample.maxpat for a simple example of a single sawtooth waveform, and wavetable_1D_sincmipmap.maxpat shows an example for a morphing wavetable.
For a long time Max, and more recently Gen, have been used extensively in industry (both large and small-scale), research centres, and community spaces to design and develop new audio-related software and hardware. (For example, Ableton Live was originally designed from a Max patch!) Today it is easier than ever to take the algorithms you write in a gen~ patch and place them into distributable~ software and hardware.
It has always been possible to export C++ code from a gen~ patch just by sending the exportcode message, but that's a pretty uncomfortable workflow. Now it is much easier because gen~ also works inside of RNBO. RNBO is a kind of re-implementation of the core of Max, including gen~, that is designed for code export from the ground-up, and has built-in support for many targets, as well as community projects for others. We have some RNBO licenses in our Digital Media lab machines that we can use for this. Or, there are other ways of exporting code and using it too -- here are some of them:
| Target | Toolchain | Description |
|---|---|---|
| Web | RNBO | It can basically be anything (a soundtrack, a soundtoy, sound for a VR world, etc.) that you can embed into a website, but you will need to code your own interface in Javascript. |
| Audio Plugin (VST, AU) | RNBO | Typically either an audio effect (sound -> sound), or an instrument (MIDI -> sound), which you can use in any typical audio software or DAW (or video editors too). It will only have a basic default interface though; to make a custom interface you can try using JUCE |
| Ableton Live device | Max4Live | Build new devices for what is probably the world's most popular digital audio software. Requires a Max4Live license; 30 day trial available. |
| VCVRack module | RNBO adapter | Create a module for this popular free virtual modular synthesizer software |
| VCVRack module | gen~ adapter | Create a module for this popular free virtual modular synthesizer software |
| Supercollider | RNBO starter | Create a unit generator (UGen) for this advanced audio programming language |
| Unreal plugin | RNBO adapter | Create a "Metasound" plugin for the Unreal game engine |
| Unity plugin | RNBO adapter | Create a plugin for the Unity game engine |
| Daisy hardware | Oopsy | The Daisy is a small Arduino-like microcontroller with high-fidelity audio support; it is now used inside many commercial (mostly independent) hardware devices (guitar pedals, Eurorack modules, desktop synthesizers) as well as lots of custom breadboard-style community projects for instruments and installations etc. Oopsy is a free/open source tool that makes it really easy to export gen~ patches to Daisy hardware. We have some Daisy-bsaed hardware available to use from the Alice Lab. See https://www.youtube.com/watch?v=fbd1CASqUmI |
| Raspberry Pi | RNBO | For custom sensor-based instruments, interactive installations, etc. Includes full support for USB Audio devices, MIDI, OSC, etc. |
| C++ code | RNBO | To embed in a custom C++ based application. It's up to you how to connect this with your other C++ code, but you could start from this RNBO/JUCE template |
| C++ code | gen~ | Just send the exportcode message to a gen~ object, and it will output some C++. It's up to you how to connect this with your other C++ code. |
Note that all of export targets will require extra work on your part to complete the project, and will require developing familiarity with the target itself. I strongly suggest taking the simplest possible examples through the export process to test them and get familiar with the process and any limitations before going any further.
Some targets are dependent on having other software installed. Some require licenses -- we do have RNBO licenses on some machines in the lab, and you can also get a trial license of RNBO to use at home. We do not have Max4Live licenses, but you can get this as part of a 30-day trial of Ableton Suite. VCVRack and Supercollider are free to install. Unreal and Unity are also free to install. You may already have software that can load VST or AU audio plugins -- pretty much any audio editor, digital audio workstation, many video editors, etc. -- many of which are free. For hardware projects, we do have a couple of Daisy-based devices available in the Alice Lab that can be used, including a guitar-pedal and some Eurorack modules, as well as bare Daisy Seed for breadboarding.
This means you will need to budget your development & testing time carefully around any access limitations!
Here's Oopsy:
Here's the example of mapping a javascript animation to sound:
Nov 20
This chapter is all about using one proess to determine the durations (or lifespans) of another. For example, a repeated tom sound has three timescales -- waveform duration (periodic), duration between sounds (periodic), and the envelope duration (a window of time):
"Hard sync" is the simplest example of one timeline controlling another timeline, by cutting the lifespan short as it "resets" it to zero. Here one phasor (scheduler) resets another (follower):
We can do this by sending a trigger to the carrier phasor 2nd inlet, and using that phasor to derive our sine wave. But this will likely lead to harsh sounds due to the jump cuts here. Bright harshness is part of the characteristic sound of "hard sync" in analog synths, but can sound worse in digital due to aliasing. (For the classic lazer sound, set the scheduler as your main frequency, and sweep the follower up and down above it.)
A simple workaround is windowed sync: just fade out the sound right before the cut, by deriving an envelope shape from the scheduling phasor (see windowed_sync.maxpat):
Comparing them on a spectroscope, the windowed-sync is certainly nicely filtered. If we sweep the follower above the scheduler now it behaves a bit more like a filter, picking out harmonics. It could be a good idea to redefine the follower frequency as an integer multiple (a "formant" or "harmonic") of the scheduler frequency.
This sounds a bit better but we are still getting aliasing -- and to understand the reason why, we need to zoom into the atomic sample level of what a phasor is supposed to be:
Notice how when a phasor resets, it doesn't usually do it at exactly the sample boundary, but somewhere between one sample & the next. If it didn't -- if it had to align right on sample boundaries -- then either we have to quantize our frequencies to divisions of the samplerate (not good!), or some waveform periods would be slightly shorter or longer than others (which causes aliasing frequencies to appear). This tiny tiny difference is audible!
In the case of our windowed sync, this means that when our scheduler resets, the follower shouldn't be reset to exactly zero, but some number slightly bigger than zero -- because by the time the sample comes we have already reset and started climbing a little. This tiny tiny difference is audible!
OK to fix the windowed-sync we need to know a) the fraction of a sample (the "sub-sample offset") that the scheduler has gone past zero, and b) multiply this by the slope of the follower to work out where it should be.
To get that sub-sample offset, we can divide the phasor ramp by its slope. Think about it: if we divide a ramp by its slope, then the result has a slope of 1. That means it adds 1 per sample -- it is a sample counter. So if it has risen to 0.3, then 0.3 samples have elapsed since it reset.
The gen~ phasor operator doesn't have a way to reset to anything other than zero, but that's ok, we know how to patch our own phasor with a history, + wrap 0 1 and a switch for the reset. We can derive our scheduler's slope either with go.ramp2slope or just by the scheduler frequency / samplerate. See windowed_sync.maxpat
Now we have an antialiased windowed sync. You can substitute any follower waveform, and any window shape, so long as the window ends at zero, and either the window or waveform begins at zero. You might notice that actually this is kind of similar to the ModFM patch we saw in Ch8, and has a similar formant-filter kind of sound. You might notice that, the more time the window is at zero, the sharper the filter-like effect.
That leads nicely to pulsar synthesis. Take the scheduler, scale it up by some "duty" ratio greater than 1, and clamp that at 1.0 to create a single shorter sub-ramp. Now use this sub-ramp to drive some carrier oscillator, and (optionally) also a window envelope to shape it:
This patch can sound remarkably like a resonant filter. It may seem strange, but the more silence between the "pulsaret" chirps, the sharper the apparent filter resonaance. Again, you have a lot of freedom in choice of the window shape, the pulsaret waveform, etc, and you can explore quite deep modulation with it too, see pulsar_FM.maxpat.
OK, but what happens if we set the window duty ratio to < 1 -- that is, if we let the window duration be longer than the scheduler period? In that case, we have a few options:
Let's look at retrigger suppression. This means we need to allow our window ramp to become independent of the scheduler phasor, as its own accumulator -- again by building our own history, +, switch circuit just like we did in the first class. Then we can simply prevent this accumulator from being reset if it is still "busy" (if it hasn't reached 1.0 yet). See pulsar_subharmonic.maxpat. Notice how setting the ratio < 1 creates new subharmonic tones -- this can be quite a musical tool (a kind of negative harmony).
OK how about the parallel overlapping option? This is a bit more involved. Strictly speaking, the CPU and the gen~ patch is only really doing one thing at once, but we need to be generating two things if two envelopes are overlapping. This is essentially like having overlapping voices in polyphony. There's a few different ways we can do this.
One of the simplest is just to create several "voice" subpatchers. If we need up to 4 sounds overlapping, which is 4-part polyphony, then we need 4 voice subpatches, and a way to dispatch events (such as "notes") to them. For example, when a new event happens, we can dispatch the event to the first voice that isn't already "busy" playing a note.
In our voice subpatch, create an inlet for the event trigger. If this voice is "busy" (the envelope isn't complete yet), we can route the trigger via a gate to an outlet, so that it can be passed onto the next voice. The voices are all arranged in a chain. The rest of the voice patch can be anything you want it to be -- any of the sound making patches we have seen so far -- and now you can make them polyphonic. (If we also output the "busy" state from a voice, then we can sum these up in the parent patch, and get a count of how many voices are active.) Also see poly_voices.maxpat and the voice1.gendsp subpatch for an example of getting many parameters into these subvoices without tons of cables.
Now we can use this exact same structure to make granular synthesizers -- which are essentially the same idea, just with event durations that microscopic, so we call them "grains" rather than note events. See the poly_granulation.maxpat patches for many examples! Granular synthesizers and granulators often use stochastic methods to schedule & parameterize their grains. Granulation often means taking some source sound, such as from a buffer~, and playing many tiny somewhat randomized fragments from that sound in dense and variegated "clouds". This is a fantastically rich souce of texture!
These are called "asynchronous" methods because the duration between events is not repetitive. If we want to do synchronous granular synthesis with grains spawned at steady audible frequencies, once gain we have to take care of the fine detail of subsample offsets. If we are driving this from a phasor, then once again, we can divide the phasor by its slope to find out how far we are past the true reset point when we start a new grain:
There's a lot of refinements we can make to this -- to handle negative frequencies, to suppress output at zero frequency, etc. which are wrapped up in go.ramp.subsample and ramp-subsample-trig.maxpat. This abstraction can replace go.ramp2trig and generates the offsets we need -- see poly_pulsar.maxpat and poly_granulation3.maxpat.
The polyphonic voice method works well but our maximum grain density is limited by the number of voice subpatches. What if we wanted hundreds of overlapping grains in a dense cloud?
The book describes a different method here, usually called overlap add, in which we "overdub the future". It's a bit like a tape delay, but now instead of having one writer and many readers, now we have one reader and many writers. Each grain is overdubbed onto the tape at a point that has not yet played, which we will hear when the tape rolls around to our read head. As the tape winds around to the reader, all of these grains get played, and then the tape at that point is immediately erased. This overlap-add method can be used for many purposes, including for building stranger kinds of delays too.
The book goes into detail with an example of overlap-add optimized for very large numbers of very short grains, in which the entirety of a grain is generated and written into the tape all at the sample moment in which the grain is triggered. This method is only viable if your grains are extremely short, but it means you can have hundreds or thousands of them. Doing this requires using codebox to create a "for loop" over the grain samples. We can also use go.ramp.subsample inputs to ensure that these tiny grains are also sub-sample accurate for pitched scheduling. See granola_buffer.maxpat and granola_glisson.maxpat.
The final section of the chapter returns to the question of anti-aliasing a sawtooth wave, using what we have learned so far. Let's just look at a raw phasor again for a minute, which is not antialiased. If you set the phasor frequency pretty high, and modulate it a little, you should be able to hear aliasing -- and see it in a scope~. Let's zoom into the atomic sample level again.
The absolute simplest movement we can imagine is a linear ramp between one sample & the next:
Notice how irregular this waveform looks -- the transition moments are irregularly spaced, and the waveform seems to wobble around. These wobbles and spacings are new lower frequencies that are not part of the ideal waveform, and this is aliasing.
It all happens because our transitions are forced to align to the sample boudnaries. But what if we could generate the same linear shape, placing the transitions between samples? Then all the irregularity disappears:
So if we can figure out how to generate this waveform, we may be able to reduce the aliasing? Looking carefullly at this, the only difference in the sample values is during the single sample in which the transition occurs.
The method taken in the book is to compute what the highest and lowest points of this shape are, and the time through this transition that occurs in a sample, so that it can linear interpolate between them. We know we can get the transition point using the same method as in go.ramp.subsample (divide ideal phasor by slope). The highest and lowest points are exactly half a sample before & after the ideal transition point.
First, we create our own phasor (again with history, +, and wrap). This phasor accumulates the slope. So we can compute what the wave would be half a sample before & after just by adding/subtracting half of the slope. That gets refined slightly to handle negative frequencies, and in the process also gives us the number of samples since the transition. When this number of samples is between 0 and 1, we are in the sample that needs to be fixed. Finally this is all plugged together with a mix to do the interpolation. See [p building] in ramp-antialiased.maxpat.
This is a really cheap way to get pretty decent antialiasing. It's not perfect, not ideal, and can be done better (with various tradeoffs) but it does a surprisingly good job for how simple it is. The book then goes on to refine the patch with two additions:
go.ramp.aa. Nov 27
Final project development & presenation
Instead of presenting final projects to class, we are instead spending today's class time refining final builds of the projects using the RNBO-enabled machines available, and I will help out with each project in any way that I can.
Instead of in-class final presentations, each team should record a video presentation that can be shared on the course website so that all of us can view them. The final deadline for the project will be Dec 6th. The deadline for the recorded presentations is Dec 12th
Exhibition
Digital Media will be having an end of term exhibition. Dates this year: December 4-6 with an opening celebration and performances Thursday, December 5 1-3pm. We need to know what works will be showing from DATT3074 (aside from submissions already made to the open call).
The deadline for us to submit work is November 30 (hard deadline), to Don by email, including:
Example of using a microphone in a web page
For the final submissions:
The deadline for all of these submissions is Dec 12th.
See you at the exhibition opening!
Further reading recommendations: