
There have been more than four decades of computational systems inspired by natural evolution. It has become a major field of machine learning and optimization. Beyond AI, it has been used in hardware and circuit design, robotics, and more recently in industrial design and architecture. It has of course also been deeply explored in art and music.

The theory of natural evolution combines population, diversity, heredity and selection:

In 1865 Mendel proposed that characteristics are transmitted to offspring through particles of matter (which we now call genetic material). Schroedinger conjectured that these materials must be aperiodic crystals, and the actual structure of DNA was identified several years later. The "modern synthesis" in biology today has integrated genetics with natural evolution, through the interaction of genotypes and phenotypes:
Hence the modern synthesis requires not only a model for how variation is introduced, but also how genetic material is transfered (inheritance) and how the phenotype emerges from the genotype (development), and what other roles it plays. It is increasingly being understood how the complexity of the environment and materials of life are likely as much or more responsible for the variety of life than the genes themselves.
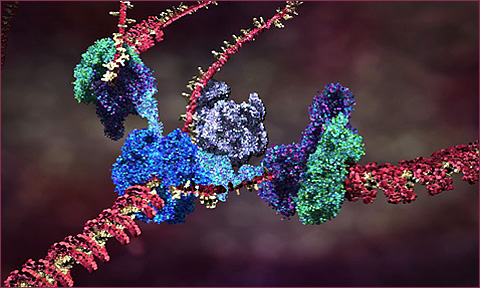
The current theory of cell replication and DNA transcription been beautifully illustrated by Drew Berry; and more of his animations here
Briefly: a biological cell contains a vast array of different proteins, whose concentrations determine structures and behaviors of the cell. The proteins are specifed by information in the DNA genetic material (grouped physically into chromosomes). When a cell reproduces by mitosis, a copy of the DNA is made in the new cell. The sections of a DNA chromosome that code for behavior are called genes. These regions are constantly being transcribed, producing a specific RNA strand for each coding gene region which is in turn used to produce a specific protein; the protein string immediately folds up (in a way we cannot yet simulate) into a particular reactive shape which specifies the protein's behavioral role in the cell. This is a one-directional flow of information: Coding DNA -> RNA -> folding -> active protein. In addition to coding regions genes may also have regulatory region which can react with specific proteins to activate or inhibit the coding-protein system, forming a complex regulatory network of interactions by which one gene can activate or inhibit another, and also specify changes of behavior of a cell according to environmental conditions such as chemical signals. These networks can be fantastically complex even in very simple organisms, according to the scientific results of functional genomics. Between the coding and regulatory regions of DNA, there are huge sections of nongenic DNA, whose role (or lack thereof) is not yet understood.
Artificial evolution is a form of computational simulation whose process emulates the abstract structure of natural evolution. Broadly it comprises:
The system is then run by these steps:
Steps 2-5 may be run in lock-step, or asynchronously with overlapping individual life-spans.
The main systematic differences between this an natural evolution are that the underlying mechanisms specified by us in advance, as are the initial populations and the method of selection and/or environmental conditions. Further, that we can stop and start, copy and replay etc. this process at will. And of course, artificial evolution occurs in a far far simpler substrate than biology!
We encountered the use of artificial evolution by Karl Sims in our introductory slides. Artist Scott Draves also produced evolutionary images as described in Scott Draves' “Evolution and Collective Intelligence of the Electric Sheep,” presented at The Art of Artificial Evolution, 2008, and more recently updated to "High Fidelity":
Evolving neural networks to play Mario:
A fantastic list of practical applications of genetic algorithm & evolutionary programming
An excellent discussion of the genetic algorithm in art and its relation to Deleuze, by Manuel Delanda
As a simple starting point, let's consider the space of simple arithmetic as our environment. Arithmietic is a good, non-trivial space because a) there are many ways to arrive at a solution, and b) there are many cases where the solution isn't obvious at the outset. It is also good, because arithmetic statements can be constructed from a very simple alphabet of terms:
let dictionary = ["+", "-", "*", "/", "1", "2", "3", "4", "5", "6", "7", "8", "9", "0"];
The selection criterion can be how effectively an arithmetic expression computes a desired target number. To make things interesting, let's make the target an irrational number, such as the value of PI:
let target = Math.PI;
Our genotype will be a list of integers (whole numbers) that can map to the dictionary:
function genotype(size) {
// initialize:
let geno = [];
for (let i=0; i < size; i++) {
geno[i] = random(dictionary.length);
}
return geno;
}
The development process, producing a phenotype from a genotype, will convert these symbols into Javascript code:
function develop(genotype) {
// convert gene values to a list of symbols:
let list = genotype.map(function(idx) { return dictionary[idx] });
// convert the array of symbols to a string of code:
let code = "return " + list.join("");
return code;
}
The chances are, the generated code is garbage, and might well throw an error. We can wrap it in a try/catch block to handle that case. It also might return a meaningless result such as Infinity or NaN, which we can detect using isFinite(). In both cases, the fitness should be zero.
Otherwise, we can measure a fitness according to how close the result is to our target. To get a value between 0 (least fit) to 1 (most fit), we can apply a 1 / (1+n) operation, where n is the absolute difference to the target:
function evaluate(code) {
try {
// convert to an executable function:
let f = new Function(code);
// run it to get the result
// if this throws an error, it jumps to the catch() below
let result = f();
// fitness is zero for Infinite or NaN results:
if (!isFinite(result)) {
return 0;
}
// otherwise, compute fitness
//according to how near it is to the target:
return 1 / (1 + (Math.abs(result - target)));
} catch(e) {
// fitness is zero if it threw an error:
return 0;
}
}
This gives us all the basic components we need to generate a random population as genotypes. We already know how to develop and evaluate such a genotype, and storing several in a population:
pop = [];
for (let i = 0; i < pop_size; i++) {
pop.push({
geno: genotype(20)
pheno: null,
fitness: 0
});
}
for (let a of pop) {
// develop genotype
a.pheno = develop(a.geno)
// evaluate fitness
a.fitness = evaluate(a.pheno)
}
It is generally useful to sort a population by fitness, which can be done like so:
// sort the population by comparing pairs
// as a result, the fittest candidate will be in population[0]
pop.sort(function(a, b) { return b.fitness - a.fitness; });
After sorting it is convenient to print out the candidates, their fitness, etc, so we can see how the evolution proceeds.
After evaluating, we create a new generation of candidates, broadly derived from the previous, but with fitter candidates being more likely to be progenitors. The simplest method is to pick a parent at random, but biasing toward the lower indices. (A simple trick to do this is for the nth child to use a the parent at index random(n).)
This is called stochastic universal sampling: it draws samples from the entire range, but selects fitter individuals more often than less-fit candidates.
We must also introduce some variation (mutations) while generating new genotypes at this point. The simplest method is to introduce a branch with a predetermined probability to randomize a gene rather than copy from the parent, e.g.:
// copy or mutate genes:
for (let j = 0; j < parent.length; j++) {
// mutate?
if (random() < mutability) {
child[j] = random(dictionary.length);
} else {
// copy:
child[j] = parent[j];
}
}
With this in play, we might already see some clear evolutionary behaviour.
But it's hard to see what's actually going on, with so many individuals flying by on each frame. To make sense of what's going on, we can introduce some statistical graphing. We can divide up the canvas into quadrants using draw2D.push().scale(0.5).translate(x, y) and draw2D.pop(), which will make it easier to separate graphs. Let's graph the following:
draw2D.rect() according to the individual fitness. draw2D.hsl() and placing an appropriate draw2D.rect(). // compute mean fitness:
let mean = pop.reduce((s, a) => s + a.fitness/pop.length, 0);
// compute standard deviation:
let stddev = Math.sqrt(pop.reduce((s, a) => s + Math.pow(a.fitness - mean, 2)/pop.length, 0))
Armed with these statistical data-visualization perspectives, and by observing the behaviour, what insights can you draw, and what ideas have you for improving it?
You may notice punctuated equilibria. Run the simulation many times (hit enter), and you may notice that the fittest candidate is not always converging to the same result. There are clearly multiple distant fitness peaks here. Does it sometimes seem to get stuck? Can you suggest why? Can you think of any way to modify the mutation, evaluation, or even the genetic representation to overcome this?
Try changing the genome size, the population size, and the mutation rates, to see how it changes.
You may notice that the code generated sometimes looks odd -- and that the evolution has discovered tricks such as adding numbers multiplied by zero, prefixing zeroes to numbers, and even placing two slashes to create a comment (followed by "junk DNA"), in order to get a result with the specific gene length. (You might even see block comments like /*7493*/!) We could easily prevent this by turning our "/" symbol into a " / " symbol, but perhaps there is an advantage not to? Even when a stable result is found, the content behind the // commments continues to change.
Math.sin()? Can you think of a way to allow different genome sizes? Can we factor in shorter genomes as a positive fitness trait?
Obviously, computing Pi is a 'toy problem', and not especially useful other than in revealing certain characteristics of artificial evolution, but the genetic algorithm can be applied to much more interesting and useful problems. What other problems could you imagine using it for? More generally, what kinds of problems might this method suited for? What kinds of problems might it not?
The genetic algorithm as presented here is one of the simplest kinds of artificial evolution; we can look at different approaches to each of its aspects, such as genetic representation, variation, selection, etc.
For problem solving in data mining, engineering, design, architecture, etc.: If the fitness criterion is static and designed around a particular problem we wish to find a solution for, evolution can help evaluate & test candidate solutions and selectively breed them to produce better solutions, ideally converging on an optimal one, without having to understand or derive by proof. It is a form of optimization. However this process may take a long time or a lot of processing power to find a satisfactory result, or may not reach a result at all. Not all problems are suitable for evolutionary search.
Note that simply taking the best candidate alone is not necessarily the ideal strategy; selecting randomly by proportion to fitness ("roulette wheel" selection) may better overcome local maxima. However many systems use a different form of selection known as tournament selection, in which a number of individuals are chosen at random from the population to create a temporary neighbourhood set, and a fitness-skewed selection is made from that set. In part this helps to mirror the spatial/network effects of populations, in that it is unlikely for every member of a population to meet every other; selection is made on the somewhat random subset of the population that is encountered. Selection pressure is easily adjusted by changing the tournament neighbourhood set size. Here's the Pi hunting example modified to use probabilistic tournament selection
Evidently, these systems differ markedly from natural evolution by having a static measure, and thus a singular teleological character, a meaningful sense of progress, across the entire history of the system. This is a pragatic approach, and highly artificial: there is no absolute or static fitness function in biology.
For art, music, and other less formalized domains we may need to consider other methods of selection, since a formal measure may not be possible, or the problem may not be clearly statable in advance. E.g. can we measure aesthetic quality in formal terms?
Biomorphs are virtual entities that were devised by Richard Dawkins in his book The Blind Watchmaker as a way to visualize the power of evolutionary processes. Dawkins used a simple symbolic rendering of lines at limited angles, grown in a kind of tree structure, as his phenotypes. Of a given generation, he selected the biomorph he found most aesthetically pleasing, making this the parent of the next generation.

Adding new lines (or removing them) based on simple developmental rules offered a discrete set of possible new shapes (mutations), which were displayed on screen so that the user could choose between them. The chosen mutation would then be the basis for another generation of biomorph mutants to be chosen from, and so on. Thus, the user, by selection, could steer the evolution of biomorphs. This process often produced images which were reminiscent of real organisms for instance beetles, bats, or trees. Dawkins speculated that the unnatural selection role played by the user in this program could be replaced by a more natural agent if, for example, colourful biomorphs could be selected by butterflies or other insects, via a touch sensitive display set up in a garden.
Check out this biomorphs recreation online!
One of the simplest ways to create a biomorph is to interpret strings as instructions for another program. The genotype is a string of symbols, the phenotype is the graphics that result. The classic example is using them as instructions for a "turtle graphics" interpreter.
We'd like to generate biomorphs in a similar way. The biomorphs are all made out of simple line drawings. For efficiency, we can use the draw2D.lines() method to draw a list of lines at once. Here's how it works:
// draws a plus (two pairs of points for each line)
draw2D.lines([
[0.2, 0], [0.8, 0], // the horizontal line
[0, 0.2], [0, 0.8], // the vertical line
]);
To draw in the Turtle style, we need to represent a turtle's properties, which are a position and a direction. Then, we can manipulate these properties to capture the turtle's movement, collecting points of a line as it moves. We can start by building a function that creates a turtle, and uses it to collect points to draw a specific shape, such as a square.
function square() {
// turtle start state:
let t = {
pos: new vec2(0.5, 0.5),
dir: new vec2(0, 0.1),
}
let lines = [];
// move forward, drawing a line:
lines.push(t.pos.clone());
t.pos.add(t.dir) // move
lines.push(t.pos.clone());
// rotate 90 degrees:
t.dir.rotate(Math.PI/2)
// move forward, drawing a line:
lines.push(t.pos.clone());
t.pos.add(t.dir) // move
lines.push(t.pos.clone());
// rotate 90 degrees:
t.dir.rotate(Math.PI/2)
// move forward, drawing a line:
lines.push(t.pos.clone());
t.pos.add(t.dir) // move
lines.push(t.pos.clone());
// rotate 90 degrees:
t.dir.rotate(Math.PI/2)
// move forward, drawing a line:
lines.push(t.pos.clone());
t.pos.add(t.dir) // move
lines.push(t.pos.clone());
return lines;
}
let lines = square();
draw2D.lines(lines);
Note: We have to be careful to insert copies of the turtle location (via
.clone()) into the list of line points. If we didn't clone a copy of the point, we would end up with many references to the samevec2object in the list.
It should be apparent that the code is highly repetitive. Conceptually, we could instead represent this as a data structure: a list of commands such as "forward, turn, forward, turn, forward, turn, forward". Let us rewrite our function as an interpreter of such a list of commands. A minimal alphabet & semantics could be something like this:
F: move forward one unit, drawing a line.+: turn a certain amount to the left.-: turn a certain amount to the right.function turtle_draw(commands, lines) {
// turtle start state:
let t = {
pos: new vec2(0.5, 0.5),
dir: new vec2(0, 0.1),
}
// interpret commands:
for (let cmd of commands) {
if (cmd == "F") {
// move forward, drawing a line:
lines.push(t.pos.clone());
t.pos.add(t.dir) // move
lines.push(t.pos.clone());
} else if (cmd == "+") {
// rotate 90 degrees:
t.dir.rotate(Math.PI/2)
} else if (cmd == "-") {
// rotate 90 degrees:
t.dir.rotate(-Math.PI/2)
}
}
}
let lines = []
turtle_draw("F+F+F+F".split(""), lines)
draw2D.lines(lines);
Now our code is not only shorter, it is far more powerful: it allows us to generate different shapes in a data-driven way, simply by passing in a different list of commands. It may already be tempting to think of what other commands we could add to this interpreter's capabilities.
With this in place, we could now expand our vocabulary of actions in our mini-language. Here are some ideas:
We could also make our shapes more dynamic. For example, we could generate rotation angles in the function according to the current time (e.g. let a = Math.sin(now)).
Turtle graphics can also create fractals, that is, objects with partial symmetries. One way of doing this is rather similar to how we created graphics state stacks with draw2D.push() and pop(): duplicating the current renderer for a sequence of operations, then returning to the prior coordinate space. With turtles being the renderer, can you imagine how to do these:
Bearing in mind what we learned with the math solver, we could go one step further and turn the interpreter a compiler; a compiler is just an interpreter that generates executable code rather than executes code. We can take our interpreter and change all of its actions into the generation of strings of code, collecting all these lines of code into a big list. Finally, we join all those strings together (with newlines and/or semicolons) and convert them into a
new Functionas before. And, rather than building strings directly, we could select operators using numbers. With this we can take any arbitrary list of numbers and turn it into a re-usable graphics function! Here's an example of how this might look:
// this is what we want to do:
let square = compile("F+F+F+F");
let lines = square();
draw2D.lines(lines);
// this is how to do it:
function compile(encoded) {
let commands = encoded.split("")
// a list to collect code as it is being generated:
let code = [
"// turtle start state:",
"let p = new vec2(0.5, 0.5);",
"let dir = new vec2(0, 0.1);",
"let lines = [];"
]
// for each command, add more code:
for (let i=0; i<commands.length; i++) {
let cmd = commands[i];
if (cmd == "F") {
code.push(
"// move forward, drawing a line:",
"lines.push(p.clone());",
"p.add(dir);",
"lines.push(p.clone());"
);
} else if (cmd == "+") {
code.push(
"// rotate 90 degrees:",
"dir.rotate(Math.PI/2);"
);
} else if (cmd == "-") {
code.push(
"// rotate 90 degrees:",
"dir.rotate(-Math.PI/2);"
);
}
}
code.push("return lines;");
// convert the resulting code into a string (with newlines)
let finalcode = code.join("\n");
// convert this into a Javascript Function:
let fun = new Function(finalcode);
return fun;
}
Since turtle graphics are generated from strings, they can be generated from string genomes! That is, we can create genotype strings as instructions for a "turtle graphics" interpreter to draw biomorph shapes. Which is therefore a function that maps genome strings into phenotypes, or into functions that create genotypes -- that is, the interpreter/compiler is the development component of artifiical evolution.
But first we need a population, and a method to generate random candidates of this population.
And, we need a way to show all the population members side-by-side or in a grid. We can re-use the draw2D.push() method to set up a grid of coordinate-frames per biomorph. If we have 16 candidates we can arrange in a 4x4 grid, using a simple method to convert population index to grid row/column and vice versa:
// get number of columns/rows from population size:
let cols = Math.ceil(Math.sqrt(pop.length))
// get row/col from population index `i`
let row = Math.floor(i/cols);
let col = i % cols;
// get population index from row, col
let index = row*cols + col;
With the above methods we can lay out the candidates in space; and, we can use the mouse to select a new individual as the parent of a new generation:
function mouse(kind, pt) {
// scale point up to grid size:
let col = Math.floor(pt[0] * cols);
let row = Math.floor(pt[1] * cols);
let index = row*cols + col;
// now create a new generation with `pop[index]`...
}
For the new generation we want to apply mutations to the chosen genotype and thus produce variants.
The example below implements a few extensions:
Remember: although we have used this method to direct a Turtle-renderer, there's no reason why the same method can be used by a very different kind of interpreter to produce a completely different paradigm of phenotypes! It could be producing forms by diffusion-limited aggregation, or voxel painting, or by directing the forces of a vehicle. It could be specifying the layout of an audio synthesizer patch or instructions for a 3D printer, etc.
The mechanisms of variation possible partly depend on the representation chosen. But one of the advantages of using lists (of symbols or numbers or genetic codes) as genotypes is the flexibility to perform many different kinds of mutations. The most common methods of variation in artificial evolution are also naturally inspired.
Random mutation; akin to errors copying DNA. For example, a parent "dog" could produce children such as "fog", "dig", and so on. Obviously some mutations will not create viable individuals.
Fragment recombination through a variety of operators (most of which are also seen in DNA):
Array.spliceArray.reverseClearly many of these mutations can change the length of the string. It may be desired to add limits on the minimum or maximum length of the string mutations can produce; or it may be desired to penalize the fitness of long strings. It is worth noting that within a biological species, DNA lengths tend to be the same, but between species there is a lot of variance in length (and not particularly correlated with the size, complexity, or evolutionary age of a species).
Why use reproduction for evolution? The main reason seems to be that crossover helps maintain diversity in the population. In the face of an unpredictable environment, we cannot know which strategy will be best; we can try small variations, and hedge our bets by making very many of them (population diversity). Unpredictibility of the world implies that what was true today may not be tomorrow, so the flexibility to avoid timeless commitment is also a good strategy; but the inheritance of choices is a useful option when the environment retains some stability. Asexual reproduction (cloning) can adapt to a habitat more explosively but also leads to more homogenous populations subject to catastrophic collapses as the enviornmental conditions change. Moreover, crossover may introduce more interesting variants than point-wise mutation alone.
As with temperature-like parameters we saw in CA, a crucial factor in evolution is the rate or probability of variation. Too much, and the population may never significantly diverge from a randomly initialized one; too little, and it may find itself stuck on the first solution it finds, with a largely homogenous population. It may be wise to have different mutation rates for mutation and recombination, for different members of a population, by fitness rank etc. Perhaps these rates can also be evolved ("meta-evolution"). Perhaps mutation rates should reduce over time unless the population appears to be stagnating. (See also simulated annealing.)
Variation may also vary per gene. Looking again at biology, we see that DNA contains certain sections that seem to be more prone to mutation than others; a gene's mutation rate itself may be an evolved/inherited characteristic. Similarly there are so-called 'jumping genes', genetic substrings that are far more likely to move location within the DNA than others. Perhaps they are functional in many locations, and can serve many purposes. In both cases, it is suggestive to consider having some kinds of markers for substrings that indicate how likely a form of mutation is at this point. How would you attempt to do this?
Neuro-evolution means using evolutionary algorithms to evolve neural networks.
A simple neural network consists of three kinds of neurons connected together:

Neurons with input connections (hidden and output neurons) compute their activation level by summing a vector of weights cross multiplied with the inputs, plus a bias term, and then feeding this through an activation function (such as a sigmoid curve). For example, if a neuron has 3 inputs, this means:
function sigmoid(x) { return 1 / (1 + Math.exp(-x)); }
output = sigmoid(in1*w1 + in2*w2 + in3*w3 + bias);
The weights (w1, w2, w3) indicate the relative importance of the inputs they are connected to. They could be zero (meaning no importance), positive (indicating a correlative relationship), or negative (meaning an inverse relationship). The bias term can act as a threshold (where weighted inputs need to overcome a negative bias to produce a positive output) or an inherent tendency (even without inputs, a positively biased neuron will 'fire').
The sigmoid function ensures that output is always bounded between 0.0 and 1.0, regardless the input. It is a smooth mapping from continous space to a bounded space, that approximates binary logic at the extremes.

So, for a specific problem, we need to know
The first two steps are usually somewhat evident from the problem at hand. E.g. if the task is to play a videogame, then the inputs would be environmental features nearby the player, and the outputs would be actions to press buttons etc. on the controller. For step 3, in many cases a fixed number of hidden layers/neurons is decided in advance (this is a "hyperparameter" of the system), and a common strategy is taken for step 4, such as connecting all nodes in one layer to all nodes in the previous layer, or to connect to a fixed number of neurons in the previous layer (both of which makes it convenient to represent weights and biases as a matrix). There isn't a general easy way to know what is the right layout and connectivity in advance, it's a bit of heuristics and trial and error.
Before getting to step 5, let's build a working neural network, and visualize the results to get an idea of what is happening. In the following example we use a simple list of numbers for the bias and weights of each neuron in turn:
The primary focus of machine learning with neural networks is deriving the weights and biases of a network that perform well in a specific problem domain. This usually involves running many generations or simulations of the network in its environment, and adjusting the weights and biases gradually to improve their performance. In supervised learning, we measure the success of a network's prediction against a training set of data of known inputs and outputs. One method to do this is called back-propagation, which involves taking the error in the output and propagating that error back through the network, using the derivative of the activation function and the weights etc., to adjust the weights of the network in a way that would reduce the error. Sometimes however a training set of data isn't available, but rather an overall cost can be measured of a neural network's performance in an environment; this kind of unsupervised learning can be effective for estimation problems. But some problems are even more complex: it may be that the error or cost of a neural network can't be taken at an individual step. For example, developing a winning strategy for a video game is only known after many steps have been taken. In these situations we can use reinforcement learning, which aims to minimize long-term "cost", balancing exploration for new knowledge and exploitation of existing knowledge.
Neuro-evolution uses evolutionary algorithms to develop neural network, in which:
the genotype needs to encode the configuration of the neural network: at minimum, the weights and biases of each neuron,
the phenotype is the executable neural network itself, whose fitness function thus depends on how well the neural network performs in the problem domain,
the performance of a neural network among a population determines its fitness for selection of a new generation.
Genetic encoding could be a direct encoding of numbers for the specific weights and biases, or could be an indirect encoding that generates the weights and biases programmatically (just as our biomorphs were generated from sequences of steps), which could also specify the network layout and connections.
For a problem domain, let's create a simple multi-agent game:
Clearly players need a few properties: a head position, a size, a tail position, a velocity, a score, and a flag to mark if they are out of the game. To begin, we can have them do a random walk, by randomly setting velocity on each frame. Updating motion for the head is the same as our simple agent systems as before. But, we have to carefully compute where the tail ends up. We can do this by getting the current head->tail vector, re-scale it to be the desired length, then addding it to the head position. This creates some interesting dynamics when an agent changes direction and reverses. We can draw the head & tail using push/pop contexts as before.
Next we add collision tests, using nested loops in a similar way as with the flocking systems, being careful not to consider ourselves. We can compute the distance between our tail & the neighbours head to see if a collision occurs. If so, the neighbour gains points, and we remove ourself from play.
So far the game works, but the agents are blind. We can give them a simple sense of vision, e.g. perhaps identifying the nearest head or tail in the world. Again we loop over neighbours (excluding ourselves), now computing the relative vector from our head to their head and tail, being careful to relativewrap() so that neighbours over the world edges are taken into account, and narrowing down to whichever has the least distance to us. To make the senses egocentric rather than allocentric, we can rotate the relative vector into our coordinate frame (so we could also use field of view limit here too, as with the flockers). It is useful to also plot this relative vector in space to understand what is happening, so we might need to store it in the agent.
Thus our new sense can identify relative orientation, relative distance, and whether the closest item is a head or a tail. To make these senses more suitable for a neural network we should normalize to 0..1 ranges:
1/(1+distance_squared), so that the sense becomes more intense as items become very close0 or 1Similarly, we must drive the motion from 0..1 parameters as the outputs of the neural network, post-scaling these as needed to drive angular change and speed. To test this, we can first feed random() into the movement. Here are a few options:
random() to set the amount of "tumble" vs. straightAgain, it is worth storing these inputs and output in the agent so we can visualize them if desired.
Try hard wiring the senses to the outputs in some variants to see what kinds of movements the mappings can generate:
Once we are happy that we have a good set of inputs and outputs, we can start adding neural networks. Each agent will have a unique set of weights and biases. The sensor data becomes the first activation layer of the network, and the final activation layer becomes the output that drives action and motion. When this works, we can run the game for a number of frames, then apply a fitness criterion for evolution based on the agent scores, sorting the population accordingly, and using it to generate a new population. Mutation would likely focus on fine or coarse adjustments of weights and biases.
Note that we might not see significant fitness improvements after the first few generations. Why? Since their environment is entirely defined by the population, than any successful strategy will quickly spread to the whole population, minimizing the relative difference. This is a self-tuning environment: they are competing against themselves, more or less. Again the "Red Queen" factor comes in to play: "running as fast as you can to stay in the same place"...
We might see a few different strategies emerge. Some hunt, some evade, some forage widely, others stay in one spot waiting for food to come to them. Try changing the rules of points scoring, e.g.:
Try changing the neural network structure
So far we have replaced entire generations at a time, but of course in the real world creatures' life spans interleave in all kinds of ways, with population booms and busts. Moreover we have rather artificially tested candidates against a pre-defined function, or against the whims of an interacting user or participant. But this isn't how nature works most of the time. As noted already, viability-based selection depends only on fundamental internal processes and exchanges with an environment (including other creatures of various species) to determine whether a creature can survive, and reproduce. So, rather than running in generations, could we try a continuous mode, where as soon as one player is removed from the game, a new player is created at a random position (with mutation from a parent taken from the current population). At this point the fitness measure of scoring points can be removed altogether: players simply need to stay in the game to have a chance of their genes being inherited.
A good starting point may be to have the genome modify parameters of the agent; for example, the amount of random walk, ranges of sensing, the reproduction threshold, thresholds of probability for selecting different actions, etc. Be careful with features like speed -- you might want to model an energetic cost to go with it for realism (and to avoid breeding supersonic agents!).
Also be careful not to oversimplify. Making a parameter of "energy efficiency" is clearly going to evolve toward maximum efficiency; there's nothing interesting about this. Things get more interesting when there are multiple constraints in play; if increasing one parameter weakens another, for example.
Similarly, a direct mapping of each gene in the genome to each parameter is likely less interesting than a more complex mapping, in which multiple processes are applied to the genome data to determine the parameters. This is exactly why the evolution of math functions was interesting: the outcome of the math function is a very complex mapping of the genes that go in. Complex enough to have surprises.
Another way of achieving this complexity in the mapping is to have the parameters drive features that have non-obvious effects or that depend on other parameters. For example, one could model a swimming organism by the speed it flaps its tail, the range it flaps over, and the average direction. Only together do these three parameters produce an arc of motion. Multiple such tails can lead to very complex motions. Similarly, taking Braitenberg's vehicles model, one could imagine placing a wire between every sensor and every motor, where the evolved parameters are the amplification weights on the wires.

For example, see Sticky Feet: Evolution in a Multi-Creature Physical Simulation -- including the video. In this example, the genome determines the structure of an organism as a set of point masses connected by springs. The springs are muscle-like in that their rest lengths oscillate, and the point masses also oscillate in their 'stickiness' (environmental friction) in order to support locomotion. Each organism has a heart and a mouth -- if the mouth of one agent touches the heart of another, it can eat it, and is rewarded by reproduction. Organisms may also have antennae attached to a spring segment, which detect either mouths or hearts, and modulate the spring length or stickiness. (A simple 3-segment creature with two sensors can very easily result in similar behaviour to the Braitenberg vehicles.)
At this point, should be clear that the effectiveness of evolution depends very much on both the genetic representation as well as its behaviour in producing phenotypes. If we consider the genetic representation as a language, then the evolutionary effectiveness depends both on the syntax and the semantics.
The syntax determines how a phenotype is encoded, what kinds of mutations are likely/unlikely/impossible, and what transformations these result in, how much space it takes up, the potential of redundancy and neutral data, and so on.
The semantics define the basic primitive concepts from which phenotypes are produced, and thus what kinds of phenotypes are likely/unlikely/impossible, including the overal size of the set of all possible phenotypes, the resolution of variations between them, and so forth. Put another way: A very common and very general method of solving problems (mathematical, computational, and otherwise), is to translate the problem into a more convenient language. We saw that our agents could reason about neighbours more easily when the neighbour poses where translated out of global space and into the coordinate space of the agent itself. Similarly, the turtle graphics language made it very easy to create simple line drawings, and with just a handful of special tokens quite complex structures, but there are still many shapes this language is unable or very unlikely to express. Simply, some languages work better than others for certain problems. (This may related to the reason why so many species share huge sequences of the same DNA.)
A good genetic representation should consider both syntax and semantics. We don't want to make our intermediate language to too restrictive, else it will not be powerful and extensible enough to encompass a wide enough range of expected and unexpected solutions. For example, we saw how creating an intermediate language of predefined words ensured we have readable (if nonsense) sentences, whereas translating into random numbers and arithmetic symbols opened the possibility of invalid expressions, but also was able to discover unexpected methods (such as using comment symbols for neutral drift). However, we also don't want our intermediate language so powerful and extensible that it becomes inefficient or intractable to actually apply, or upon which evolution has barely a chance to have impact. Our math & turtle graphics examples demonstrated how using a programming language as intermediate representation can achieve great power/diversity with succinct syntax.
Naturally environmentally-based viability selection has also led to models of ecological or ecosystemic basis. A simple starting point may be to take the agent-based example of variable populations with energy-exchange and preservation, and add genetics. In this case viability is principally determined by energy maintenance, so we have to take extra care in modeling this well. Every action an agent takes must cost energy, and this should be proportionate to the action taken. Sprinting takes more energy than sauntering. Locomotion models can estimate energy cost from the force actually applied; which is exactly the acceleration multiplied by the mass. We can approximate this by taking the difference between current & new velocities (after all clamping) and multiplying by the organism size. It may also be wise to have a basic metabolism cost to remain alive, that perhaps may increase with size, and with age.
Here's a start in this direction
As organisms evolve better strategies, they can better utilize the finite energy resources of the world, and thus support greater populations. An adaptive difficulty, perhaps applied to the metabolism cost, or applied generally to the available energy in the world, may help keep selection pressure effective at maintaining population size. For example, we can gradually decrease the total energy in the ecosystem while populations are large, and increase it again while populations are small.
Note that exactly how new energy is introduced can have quite drastic effect on the adaptive conditions -- since effectively organisms are trying to evolve strategies to be more viable, the distribution of energy in the world is the primary factor. The simplest option is to reintroduce the energy immediately, spread uniformly over the space, e.g. field.add(energy_deficit/(field.width*field.height)). More interesting behaviours can emerge when energy is redistributed more gradually and non-uniformly in space.
Given a model of an agent as comprising a collection of sensors, a collection of internal nodes of computing (such as a neural network), and a number of output nodes (as actuator potentials) that cause actions in the world, which could be extended in a few ways:
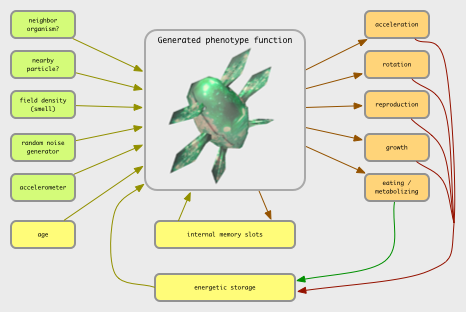
Possible inputs include:
Possible outputs include:
If it is helpful, you may imagine the buttons you can press to control a videogame character. Each button is an output.
Possible action structures:
Event-like inputs can be treated as signals whose value is zero when no event is occurring. Event-like outputs can be treated as signals that pass a given threshold, or change by a significant margin. Thresholding is a general way to convert a signal to an event, possibly with some accumulation & relaxation time, and sampling is a way to convert an event into a signal, possibly with some averaging/smoothing.
Normalization:
Possible internal operations:
The middle layers between inputs & outputs may utilize a palette of mathematical mappings and simple signal-processing operators, or a neural network model as we have above, or a combination of both. For example, the set of "neural nodes" available in Karl Sims' evolving virtual creatures simulation included:
sum, product, divide, greater-than, sign-of, min, max, abs, if, interpolate, sin, cos, atan, log, expt, sigmoid,
Furthermore, a number of more complex "stateful" operators (i.e. operators which include their own history/memory) were included:
sum-threshold, integrate, differentiate, smooth, oscillate-wave, and oscillate-saw.
Sum-threshold refers to a unit that operates much like a real neuron, accumulating inputs until a threshold is reached, then outputting a pulse and relaxing to zero. That is, neural networks are often modeled using only the sum-threshold (or even simpler, sigmoid) operators. Integrate is a simple counter, but it may be wise to make it "leaky", such that the accumulated value naturally decays over time. Smooth is a simple moving average, or low-pass filter, such as averaging the current and previous input. The oscillators are a combination of a counter with a trigonometric or modulo operation.
Other kinds of internal operations could be structural, such as creating a sequence of actions (and possibly including policies to abort a sequence if an action cannot be completed) or a sequence of options (taking the first one that can be executed).
Darwin's theory is sometimes misconceived as "survival of the fittest" or even the competitive "law of the jungle", but evolution turns out to be quite a bit more subtle than this.
First, the notion of "fittest" is misleading. It implies a static and absolute measure against which all individuals and species in the biological record can be compared. In natural evolution there can be no pre-defined fitness measure. This is because the environmental conditions are highly dynamic, and thus selective criteria are quite contextual. The conditions in which we live evolve along with us, and the other species in our habitat, as we mutually influence each other. Evolution is an open-ended process.
Evolution does not imply a continuous process of change. The fossil records appear to show long periods of relative stability divided by relatively brief periods of biological invention. There are several competing theories as to why this is, but interestingly this "punctuated equilibrium" has appeared also in many artificial evolutionary systems.
An individual organism does not need to be optimally fit to the environment in order to contribute to the gene pool -- it simply needs to be fit enough to reproduce, i.e. to be viable. A natural species depends only on the viability of enough individuals to reproduce within an unpredictable environment.
Competition turns out not to be the prime mode of interaction between species; most species seem to have evolved to be relatively independent of each other, and the ones that do closely interact are more likely to be collaborative than competitive, through symbiosis or other means, as that is more likely to lead to viability. Evolution does not imply that individuals display selfish behavior.
To support diversity, an environment must be complex enough to provide multiple methods of making a living (evolutionary "niches"). There is a cybernetic theory that, for life to take advantage of the variety of niches present in an environment, and the variety of problems to overcome, life must have a corresponding requisite variety with which to adapt; that is, sufficient potential diversity.